 
ここでは、モーション・シンセサイザーの原理について説明していきます。
数式を極力使わずに、イメージを用いて直観的に説明してみようと思います。
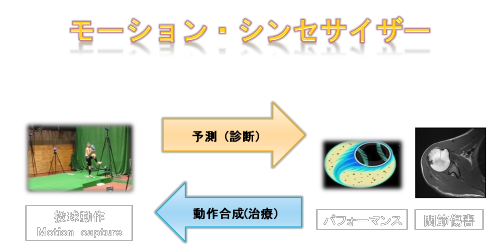
モーション・シンセサイザーでは、投球動作をモーションキャプチャすることにより、
パフォーマンスや障害を予測することができ、
障害を防ぎつつパフォーマンスを高めていく投球動作をコンピュータ上でシミュレーションすることができます。
この双方向性の計算をどのようにして行っているかを、一緒にみていきましょう。
少し長い道のりですので、マイペースでお読みください。
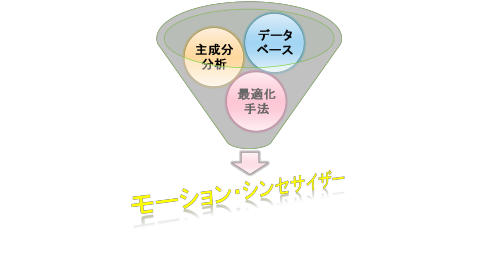
モーション・シンセサイザーは
① データベース
② 主成分分析
③ 最適化手法
の3つから成り立っています。
これから順番に述べていきます。迷子になったらこの図を思い出しましょう。
モーション・シンセサイザーでは、データベースを客観的に解析することでシミュレーションを作成します。したがって、まずはデータベースの構造を理解することからはじめていきます。

まず、データベースの中身です。
無症状の社会人野球選手と大学野球選手を対象に、
MRI撮影、投球動作のモーションキャプチャ、球速の測定、球の回転数と回転軸の計測コントロールの評価を行い、これらの情報をデータベース化しました。
現在のところ(2013.10)、データベース内の投球試技数は約400試技です。
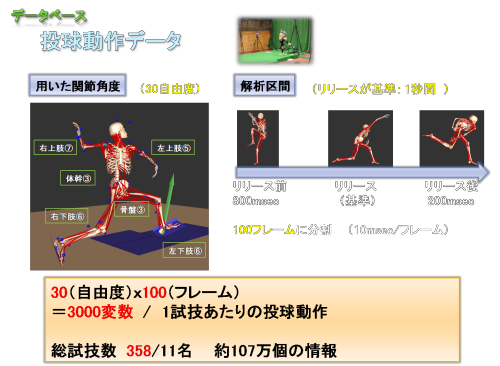
データベース内では、投球動作データが最も大きな情報量を持っています。
変数量としては、約3000変数あります。その内訳を説明します。
投球動作を表現するのに、30個の関節角度を使っています。
例えば、右上肢は7個の関節角度を使っています。その内訳は
①肩内外転②肩水平内外転③肩内外旋④肘屈曲
⑤前腕回内外⑥手掌背屈⑦手撓尺屈
といった具合です。
解析区間は
ボールリリースを基準として、その前後1秒間としました。具体的には
リリース前800msecからリリース後200msecまでを時間で正規化し、
この区間を100フレーム(10msec/フレーム)に分割しました。
そうしますと、1試技あたりの投球動作には
30(関節角度)x100(フレーム)=3000(変数)
もの変数を認めることになります。
さらにデータベース内には、投球動作データの他に、MRI、球速、球の回転数と回転軸、コントロールのデータも入っていますから、データベース内の総変数は
3000(変数)+α
の変数が存在します。
例えば、データベース内の社会人野球選手の総試技数は358試技ありますので、
(2012年当時、現在はどんどん増加中)
3000+α(変数)x358(試技)で
データベース内には、社会人野球選手のデータだけでも最低100万個以上の情報が存在します。

さて、データベースの構造が理解できたところで、モーション・シンセサイザーの解析原理を説明していきます。解析の手順としては、まず主成分分析を行い、つぎに最適化計算を行っていきます。
通常主成分分析などの説明には、数式を用いて説明する書籍が多いですが、
ここでは数式を極力使わずに、イメージを用いて直観的に説明してみようと思います。

解析原理のキモの目次を上記に記載しました。
解析原理のキモは全部で5つありますが はじめのⅠ~Ⅳまでが主成分分析に関することで、Ⅴは最適化手法に関することになります。
一つ一つ説明していきますので、マイペースで理解していきましょう。
迷子になったときは、この目次に戻りましょう。
 |
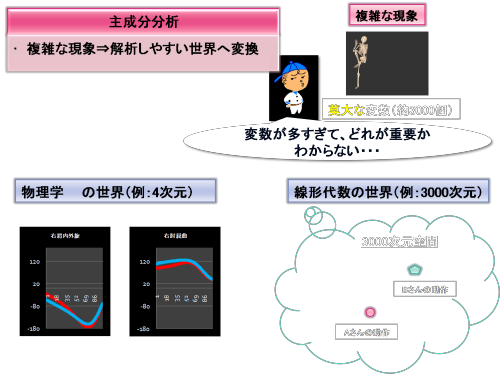
投球は非常に複雑な現象です。さきほどデータベースの構造の話をしましたが、データベース内には投球動作だけで約3000個もの変数があります。
これだけ変数が多いと、
「変数が多すぎて、どの変数が重要なのかよくわからない」
ということが生じます。
そこで、この複雑な現象を解析しやすい世界へ変換することを考えてみましょう。
仮に、投球現象を物理学の世界で表現したとします。
物理学の世界は4次元(3次元空間+時間)ですから、
縦軸:関節角度 横軸:時間
というグラフを作成しますと、上図のような曲線のグラフが30個あまり並ぶことになります。この30個もある曲線のグラフを解析することは、「非常に難しい!」です。
今度は、投球現象を線形代数学の世界で表現してみます。
線形代数の世界では次元を拡張することができます。そこで、今回は3000次元空間という世界を考えてみようと思います。いきなり、「3000次元空間」と言われてもイメージすることは難しいでしょう。一般的に人間は、4次元空間まではイメージできますが、5次元空間以上はイメージできないことが普通です。ただ、線形代数学では3000次元空間というものを考えることができ、そうした次元拡張した世界でも通用する学問なのです。
なぜ、こんな3000次元空間とういものを考えるのでしょうか?
それは、3000次元空間では「ある1試技の投球動作を1つの点」で表すことができるからなのです。
今、データベース内に400試技の投球動作があったとすると、
3000次元空間ではこの400試技の投球動作を400個の「点」で表せます。
「曲線」と「点」 : どちらが簡単に解析できるでしょうか?いうまでもなく「点」です。
モーション・シンセサイザーの解析の1番目のキモ・・・
現実世界の複雑な現象を線形代数の次元拡張した世界で考えることによって、
複雑な現象を「点」の分布で表し、解析をしやすくしていきます。


さて、今は主成分分析の部分です。解析原理のキモのⅠの説明が終わりましたので、次はⅡの説明をしていきます。
 |
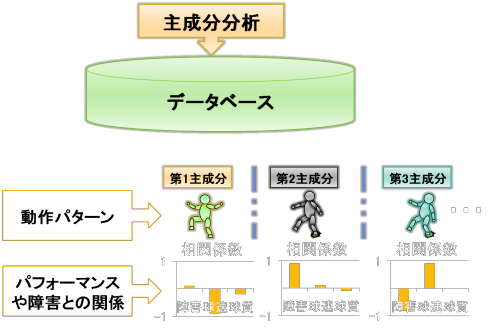
この節では、投球動作パターンを客観的に分類して、そのパターンとパフォーマンスや障害との関係を調べていく方法論を説明します。
動作パターンを分類できれば、投球現象がどのようなパターンから構成されているかという枠組みがわかります。
そして、1つ1つのパターンを組み合わせることで、既存の動作を作り出すことも、新しい動作を作り出すこともできるようになるのです。これがモーション・シンセサイザーの根幹部になります。
今回は主成分分析を行うことによって、投球動作のパターンを客観的に分類していきます。統計学的に客観的にパターンを求めるためにはどのようにしたらよいのでしょうか?ここでは、数式を使わず、イメージで直観的に説明します。
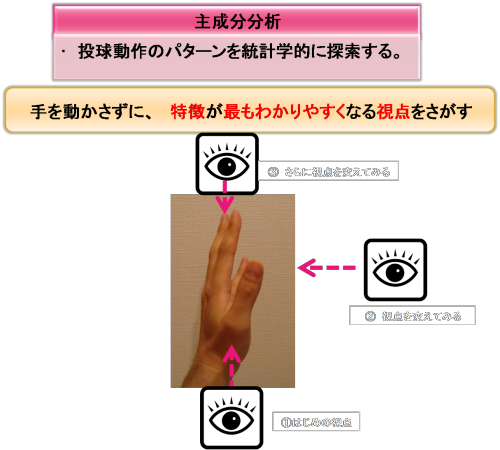
まず、簡単な例をやってみましょう。上図のように左手を目の前に置いてみてください。左手の親指、示指、中指、環指、小指が情報だとします。今の状態は左手のそれぞれの指は重なってみえると思います
我々は、これが左手の指であることをあらかじめ知っていますが、もしもそうした先入観がなかったとしたら、それぞれの指は重なっているため、特徴がややわかりにくいと思います。
さて、この状態で左手を動かさずに、左手の特徴が最もわかりやすくなる視点はどこですか?
と問われたら、どこから左手を観察するでしょうか?実際にやってみてください。
②の視点から左手を観察すると、左手の特徴が最もわかりやすくなるでしょう

先図で、②の視点から、左手を観察すると上図のようになると思います。
この視点では、左手のそれぞれの指は、まったく重ならずにばらついて、それぞれの指の特徴が最もわかりやすいと思います。
これを今度は数学的に表現していきます。
「手を動かさずに」とは、「データをいじらない。データを加工しない。」ということを意味します。主成分分析では、「視点を変えているだけなので、生データそのものに操作は加えておりません。」
「最も特徴がわかりやすくなる視点」とは、「最も分散が大きくなる軸」を意味します。これを第1主成分(パターン)と呼びます。
分散は、データのばらつき具合を意味しますから、第1主成分(パターン)とは、最もデータのばらつきが大きくなる軸を意味します。
主成分分析ではこの第1主成分(パターン)をまず探索していきます。
主成分分析を投球現象にあてはめると、
「投球動作の特徴が最もわかりやすくなるパターン」
をまず探索するということになります。
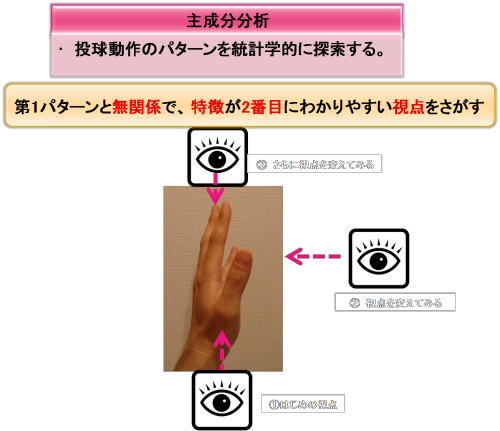
はじめの視点に戻ります。それでは今度は、
第1主成分(視点②)と無関係で、2番目に特徴がわかりやすくなる視点はどこですか?
と問われたら、どこから左手を観察しますか?実際にやってみてください。
おそらく、③の視点から左手を観察すると、第1主成分(視点②)と無関係でかつ左手の特徴が2番目にわかりやすくなるでしょう。

先図で、③の視点から、左手を観察すると上図のようになると思います。
この視点では、左手のそれぞれの指は、あまり重ならずにばらついて、それぞれの指の特徴が2番目にわかりやすいと思います。
そして、第1主成分(パターン)とはまた違った感覚で観察できるでしょう。第1主成分(パターン)の視点②とは直交した位置から見ているからです。
これを今度は数学的に表現していきます。
「第1主成分(パターン)と無関係で」とは、「第1パターンの影響をうけずに、独立している」ことを意味します。これを幾何学的に表現しますと「第1主成分軸と直交する」ことを意味します。
「2番目に特徴がわかりやすくなる視点」とは、「2番目に分散が大きくなる軸」を意味します。分散はデータのばらつき具合を意味しますから、第2主成分(パターン)とは、2番目にデータのばらつきが大きくなる軸を意味します。
つまり、第2主成分(パターン)とは第1主成分軸と直交し、2番目にばらつきが大きくなる軸です。これを投球現象にあてはめれば、
「投球動作の第1パターンとは無関係で、2番目に特徴がわかりやすいパターン」
ということを意味します。
以後、これと同じ作業を3000回繰り返すことにより、3000個の主成分(パターン)が抽出されます。
今回の例題は現実世界の3次元空間で行っていますから、3つの軸しかイメージできませんが、線形代数の世界では3000次元空間というものを考えられますから、3000個の主成分軸を求めることができるのです。
コンピュータが発達した現在、こうした作業はすべて統計ソフトがやってくれますから、人間は数回クリックするだけで、データベース内のパターン化を数分以内に完了できます
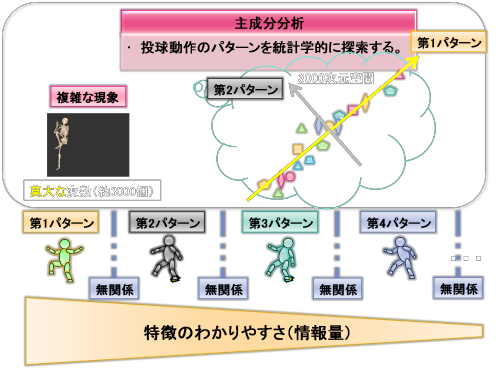
さて、これまでに3000個もの主成分軸(パターン)を求めてきました。主成分分析の定義から、これらのすべての主成分(パターン)はお互いに無関係です(直交しています)。
そして、各主成分は特徴のわかりやすい順(分散の大きい順)に並んでいます。
数学的には3000個もの主成分(パターン)を抽出しましたが、実際現場では有用な主成分(パターン)は10個ほどで、多くても第1主成分から第10主成分ぐらいまでです。
これらの主成分(パターン)は特徴のわかりやすい順に並んでいますから、残りの第11主成分から第3000主成分までの2990個の主成分は実は不要になります。
このように、主成分分正では情報量の大きい主成分(パターン)を数学的に順番に抽出します。これを投球現象にあてはめれば、
「現場で有用な動作パターンを重要度が高い順に抽出し、不要なパターンを無視することができる」
ことを意味します。
以上、データベース内の投球動作パターンを統計学的に客観的に分類してきました。


さて、今は主成分分析の部分です。解析原理のキモのⅡの説明が終わりましたので、次はⅢの説明をしていきます。
 |
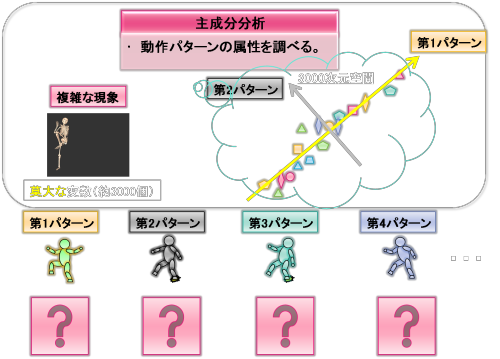
これまでは、データベース内の投球動作パターンを統計学的に客観的に分類してきました。分類されたそれぞれの動作パターンは、パフォーマンスや障害とどのような関係があるのでしょうか?
これを調べるためには、各主成分軸周りにどのようなデータが分布しているかを調査し、各主成分の属性を相関係数で表していきます。
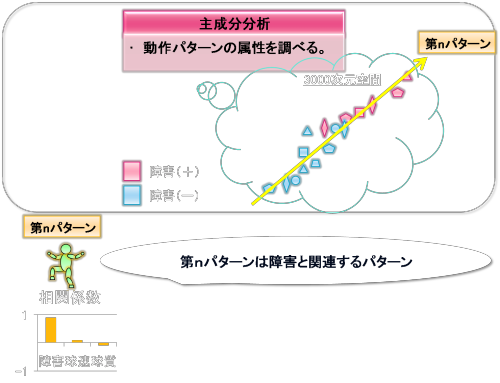
例えば、第n主成分軸周辺のデータの分布が上図のようだったとします。
第n主成分軸の右にいけばいくほど「障害(+)」、左にいけばいくほど「障害(-)」が分布していることが読み取れます。
主成分分析では、
主成分軸に沿って右にいくことは主成分得点が増加することを意味します。
主成分軸に沿って左にいくことは主成分得点が減少することを意味します。
したがって、第n主成分軸において主成分得点と障害との相関関係を調べますと相関係数はかなり高くなるはずです。
このとき、第n主成分(パターン)は障害と関連するパターンであり、第n主成分の
主成分得点を増やす(右にいくと)と障害ができやすく、
主成分得点を減らすと(左にいくと)障害ができにくく
なると解釈されます。
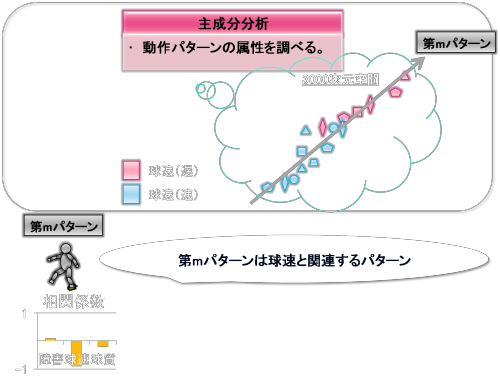
もうひとつ例題を出します。
例えば、第m主成分軸周辺のデータの分布が上図のようだったとします。
第m主成分軸の右にいけばいくほど「球速が遅く」、左にいけばいくほど「球速が速い」が分布していることが読み取れます。
主成分分析では、
主成分軸に沿って右にいくことは主成分得点が増加することを意味します。
主成分軸に沿って左にいくことは主成分得点が減少することを意味します。
したがって、第m主成分軸において主成分得点と球速との相関関係を調べますと相関係数はかなり低く(マイナス)なるはずです。
このとき、第m主成分(パターン)は球速と関連するパターンであり、第m主成分の
主成分得点を増やす(右にいくと)と球速が遅くなる、
主成分得点を減らすと(左にいくと)球速が速くなる
と解釈されます。
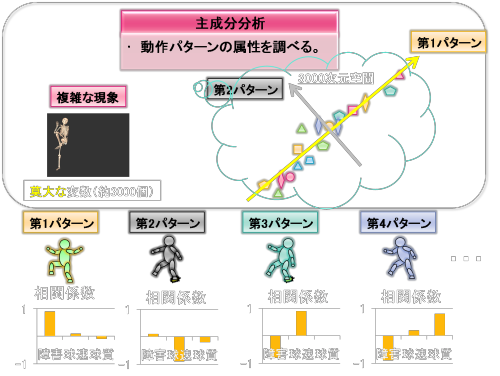
同様のことを繰り返すことによって各パターンの属性を調べていきます。上図では
第1主成分(パターン)は障害に関与する(主成分得点が増えると障害が増える)
第2主成分(パターン)は球速に関与する(主成分得点が増えると球速が減る)
第3主成分(パターン)は障害と球速の両者に関与する(主成分得点が増えると障害が減り、球速が増える)
第4主成分(パターン)は障害と球質の両者に関与する(主成分得点が増えると障害が減り、球質が高まる)
などのように解釈されます。
以上、データベース内の投球動作パターンについて、それぞれのパターンの属性を調査してきました。


さて、今は主成分分析の部分です。解析原理のキモのⅢの説明が終わりましたので、次はⅣの説明をしていきます。
 |
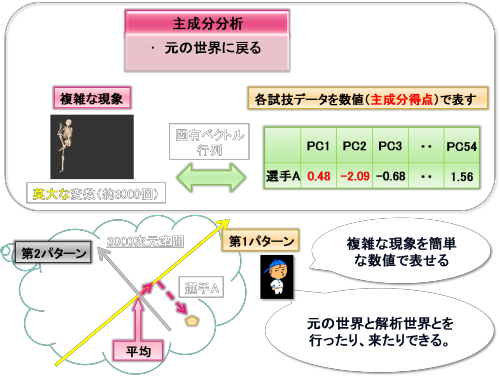
さて、これまでは、現実の複雑な投球現象を線形代数の世界で考えることによって、解析しやすくしてきました。そして、動作パターンを客観的に分類し、各動作パターンがどのような属性を有するかを調査してきました。ここでは、主成分分析のその仕組みをもう一度再確認し、これをどのようにシミュレーションにつなげるかを述べます。
投球動作は複雑な現象であり、データベースでは3000余りの変数から構成されいます。主成分分析を行うことで、投球動作パターンを客観的に分類し、それらのパターンを特徴のわかりやすい順に並べました。そして、それぞれのパターンは互いに直交し、独立しているということを説明してきました。
主成分分析を行うとデータベース内の任意の動作は、主成分得点という簡単な数値で表せるようになります。上図をみてください。たとえば、
ある選手の投球動作は
第1主成分得点(PC1)が0.48、第2主成分得点(PC2)が-2.09です。
これは3000次元空間において第1主成分軸と第2主成分軸からなる平面で考えたとき、平均から第1主成分軸に沿って0.48移動し、次いで第2主成分軸に沿って-2.09移動したところに選手Aのデータが存在していることを意味します。
統計ソフトで主成分分析を行いますと、各選手の主成分得点も自動的に算出してくれます。はじめは、主成分得点とは各選手の動作を動作パターンごとに点数化したものだと単純に考えてもらえればよいかと思います。
さて、主成分分析を行いますと、固有ベクトル行列というものも自動的に算出されます。
「データベース内の情報」----「固有ベクトル行列」----「主成分得点」
データべースの情報と主成分得点は固有ベクトル行列を介して、お互いにつながっています。データベースの情報から固有ベクトル行列を介して、ある選手の動作の主成分得点を求めることができますし、ある主成分得点から固有ベクトル行列を介して、データベース内の情報を求めることもできます。
つまり、主成分分析では固有ベクトル行列を介して、データベース内の情報と主成分得点を双方向性に計算することができるのです。このことを比喩的に表現すれば
データベースの情報は「現実世界の複雑な現象」を表し、
主成分得点は「解析しやすい世界の動作パターンの点数」を表し、
固有ベクトル行列は「現実世界と解析世界をつなぐ地図」を表します。
主成分分析のこうした性質を利用することで、元の世界と解析世界とを自由にいったりきたりできるのです。そして、この性質を利用することでシミュレーションを作成できるのです。
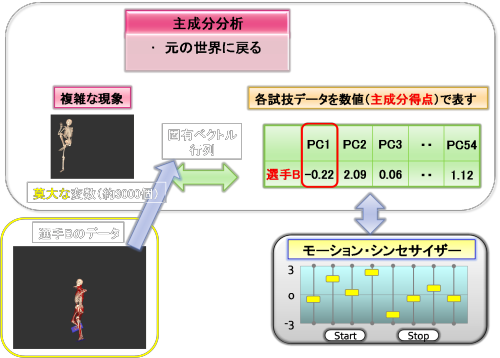
さきほどの説明はやや抽象的だったので、もう少し例をだして、説明します。
上図のように今データベース内に選手Bの投球動作データがあるとします。このデータに固有ベクトル行列を掛け合わせると選手Bの主成分得点が求められます。
次に、この主成分得点に対応するスライドバーを作成します。
ここで、第1主成分(PC1=-0.22)に着目して、この主成分得点を変更するとどうなるでしょうか?
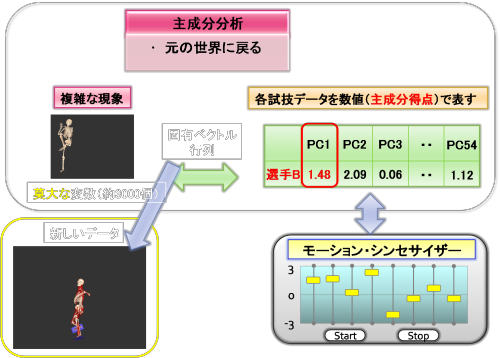
上図のように第1主成分のスライドバーを動かして、PC1の主成分得点を先ほどの-0.22から1.48に変更したとします。
さきほど述べたように、データベースの情報と主成分得点は固有ベクトル行列を介して双方向性に計算できますから、今度は変更した主成分得点に固有ベクトル行列を掛け合わせていきます。すると、今回の第1主成分得点の変更に応じた新しいデータが生成されます。
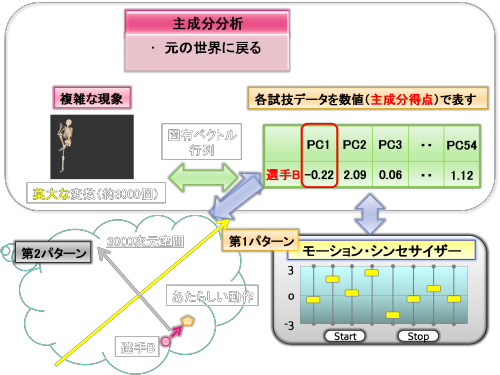
これを3000次元空間の線形代数の世界で表現したのが上図です。
3000次元空間内では選手Bの投球動作は点で表現されています。
スライドバーの第1主成分得点の部分を-0.22から1.48に変更することは、
3000次元空間内で第1主成分軸に沿って、「選手Bの点」を「あたらしい動作の点」まで移動させたことを意味します。
このように、モーション・シンセサイザーでは主成分得点のスライドバーをさまざまに操作することによって、さまざまな動作データをあたらしく作り出すことができるのです
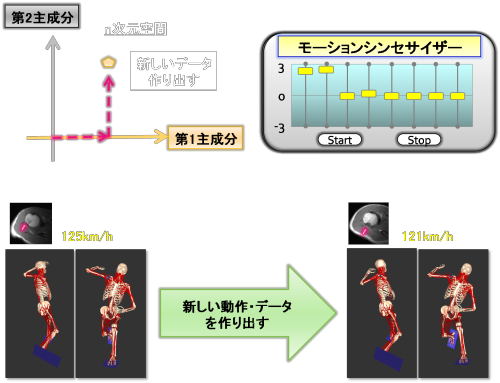
モーションシンセサイザーのもうひとつの重要な特徴を最後に述べます。モーション・シンセサイザーではそれぞれの主成分(パターン)をベクトルの演算のように合成することができます。
例えば、上図のように第1主成分と第2主成分のスライドバーを移動させて、主成分得点を変えたとします。これは3000次元空間内では、直交する第1主成分と第2主成分からなる平面内で、第1主成分のベクトルと第2主成分のベクトルを足し合わせたものに相当します。このように、モーション・シンセサイザーではさまざまな主成分同士を合成し、新しい動作データを作り出すことができます。


さて、これで主成分分析の部分の説明は終わりました。次は最適化手法です。
解析原理のキモのⅣまでのの説明が終わりましたので、次はⅤの説明をしていきます。
 |
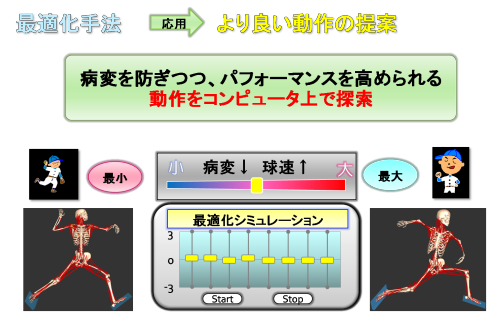
現場のニーズに複合的に応えていくことがこのシステムの最終目標になりますので、最後は、目的(ニーズ)に合うパターンを探索していきます。
ここでは、数学的最適化手法を用いることで、よりよい動作というものを提案していきます。例えば、「病変を防ぎつつ、球速を高める動作を求めたい」というようにニーズを設定したとします。
モーション・シンセサイザーでは、最適化計算を行うことでニーズが最大になる動作やニーズが最小となる動作をコンピュータ上で探索し、探索した結果を3Dアニメーションで表現することができます。
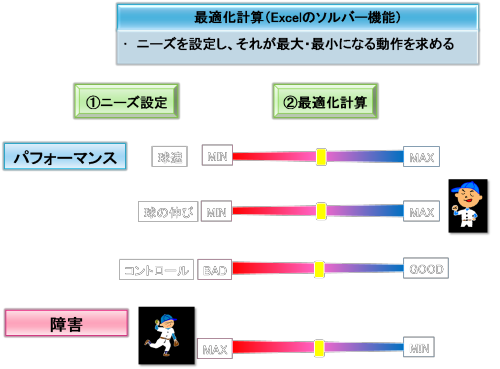
最適化計算を行うのに先立ち、まずはニーズの設定を行います。ニーズの設定は、上図のように仮想のスライドバーを動かして行います。
例えば、
球速を高める動作を求めたいときは、球速のスライドバーをMAXに近づけていきます。
球が伸びにくい動作を求めたいときは、球の伸びのスライドバーをMINに近づけていきます。
コントロールを悪くしたくないときは、制約条件にコントロールが低下しないように設定することができます。
障害を防止しつつ、球速を高めたいときは、障害と球速の両方のスライドバーを操作します。
このように、さまざまなニーズの設定を行うことができ、こうしたニーズを組み合わせた設定を行うこともできます。
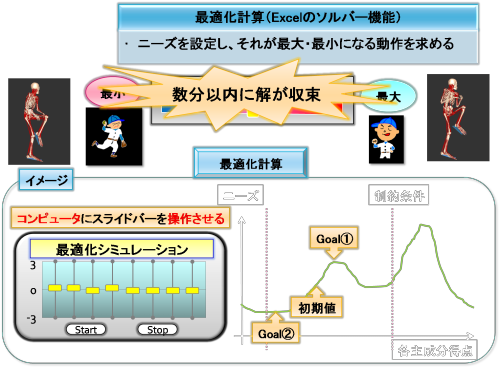
最適化計算は利便性の観点からExcelのソルバー機能を使っています。
上図は最適化計算を直観的にイメージしたものです。
モーション・シンセサイザーのスライドバーをコンピュータに片っ端から操作させていきます。初期値(もともとの投球動作)と制約条件を設定した後に、計算を開始します。
制約条件下で、ニーズが最大となる主成分得点の組み合わせを求めます。
制約条件下で、ニーズが最小となる主成分得点の組み合わせを求めます。
これらは、すべてコンピュータが高速で行ってくれます。
最適化計算にかかる時間は、数秒から数分くらいです。(計算にかかる時間はデータベース容量やコンピュータのスペックに依存します)
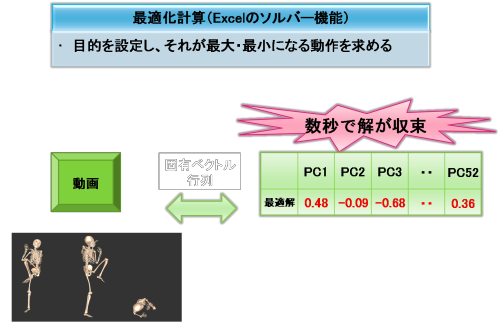
コンピュータが探索した最適な主成分得点の組み合わせが求められたら、固有ベクトル行列を介してデータベースの情報に変換します。
本システムではこのシミュレーションされた結果を投球動作の3Dアニメーションとしてさまざまな視点から閲覧することができます。
 |


まとめです。モーション・シンセサイザーの解析原理を5つの手順を踏んで述べてきました。このシステムは、データベースさえあれば投球動作に限らずさまざまな動作に応用することができます。そして、スポーツに限らず、心理学でも医学でもさまざまな現象に応用することができるのです。
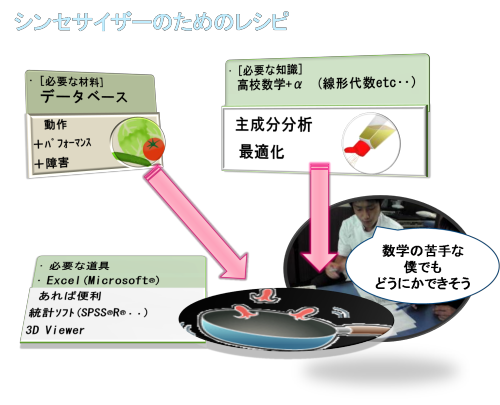
モーション・シンセサイザー理論体系はほぼ確立しました。
作成のレシピですが、
必要な道具は Excel、統計ソフト、3Dビューワーだけでできます。いずれもそれほどお金はかからずにできるでしょう。
必要な材料はデータベース。どんなデータベースでも応用可能です。
必要な知識は線形代数などの高校数学の知識に主成分分析と最適化の知識だけです
したがって、この手法は勉強さえすればだれにでもできる方法です。原理をしっかり押さえて、ぜひいろいろな分野でチャレンジしてみてほしいと思います。
 
|